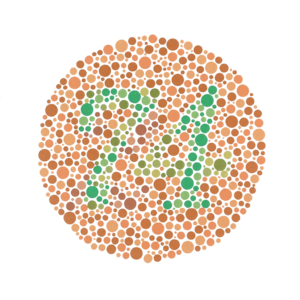CISC181 S2019 Lab2
Preliminaries
This assignment uses the Swing library for basic drawing. You may want to refer to the documentation for the JFrame, JComponent, Graphics, and Color classes, among others. Just like last time:
- Make a new project (but now n = 2) following these instructions.
- Name your class "Lab2". This happens when you are creating a new module, in the Java class name field
Instructions
Modify Lab2.java as follows:
- Add your name and your partner's name in a comment before the Lab2 class body, as well as each public class you create (i.e., the custom JComponents outlined below)
- Initialize a different JFrame and custom JComponent (as explained in the Swing portion of the Feb. 26 lecture slides) for each of the two exercises below
- Here is some example code used in lab. This is just to start -- you will be adding a lot to it.
- Each custom JComponent will have its own paintComponent() method doing something different for each exercise below
- Two JFrames initialized in main() means two windows should pop up each time you run the program
ColorJComponent
For this exercise you will draw several patterns similar to an Ishihara-style color blindness test. The basic idea is that many randomly-sized circles are drawn, with a number or other meaningful pattern distinguished by some circles being colored differently from the rest. An example of such a test is shown below:
You are not going to draw numbers, but rather several simple shapes: either a large circle, square, or a diamond. We provide a ColorJComponent.java class to use as a template. This class already draws randomly-placed, randomly-sized, non-overlapping circles, as shown below:
Your job is add code to the class to color the circles in as follows:
- The window should be drawn with a white background
- Each time paintComponent() is called, you should randomly decide whether the hidden shape to be drawn is a circle, square, or diamond. The hidden shape should be centered in the window, and if it is a square or diamond, its sidelength should be half the window width. If a circle, its diameter should be half the window width.
- Each small circle should be filled with a randomly-chosen RGB color as follows:
- If the current "hidden shape" is a circle: If the small circle's center is inside the shape, draw it with a random RGB in the green/light-green range. If it is outside the shape, choose a random RGB in the red/orange range.
- If the current "hidden shape" is a square: If the small circle's center is inside the shape, draw it with a random RGB in the orange/yellow range. If it is outside the shape, choose a random RGB in the cyan/green range.
- If the current "hidden shape" is a diamond: If the small circle's center is inside the shape, draw it with a random RGB in the pink/lavender range. If it is outside the shape, choose a random RGB in the light gray/dark gray range.
The process of randomly selecting the potential colors for the circles should occur ONCE, in the constructor -- not paintComponent(). You will need to store the results somewhere (maybe an array, hint, hint????) and look them up each time you draw.
Finally, the positions and sizes of the filled circles should be scaled proportionally if the window changes size (which you will know because getWidth() and getHeight() will return different numbers).
Extra credit: can you figure out how to use arbitrary characters (appropriately enlarged) as the hidden shapes?
GraphJComponent
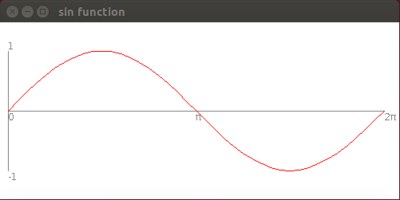
For this exercise you will draw a portion of a graph of the sine, cosine, and tangent functions.
Your graph should have the following characteristics:
- The window will initially be 500 x 250, have the title "Trigonometric functions", and have a white background
- The plot should be scaled to more-or-less fill the window (i.e., don't use the 500 and 250 numbers directly for dimensions, but rather getWidth() and getHeight() in case the window is resized)
- The plot covers the range from 0 to 2π radians horizontally, and approximately -3 to +3 vertically (the image shown only has -1 to 1 -- don't just duplicate it!)
- Draw the sine curve in red, cosine curve in blue, and tangent curve (or curves, because of discontinuities) in green. A straightforward way to do this is as a series of connected line segments (perhaps with drawLine() in a loop). Make sure to use enough segments that each curve is somewhat smooth.
- Draw a horizontal and vertical axis in gray as shown
- Label the vertical axis with "-1", "-2", "-3", "1", "2", and "3" where appropriate
- Label the horizontal axis with "0", "π/2", "π", "3π/2", and "2π" where appropriate. "π" should be drawn as a Greek letter (the Unicode is '\u03c0')
You may add more labels, tick marks, dashed asymptotes, etc. to your plot as desired -- the above represents minimum requirements.
Finishing up
Remember to use proper naming and formatting style throughout your code, and submit your Lab2.java, ColorJComponent.java, and GraphJComponent.java on Canvas by midnight (or just after) on Tuesday, March 5